Unpaired Weyl Point observed for the first time in crystalline solid

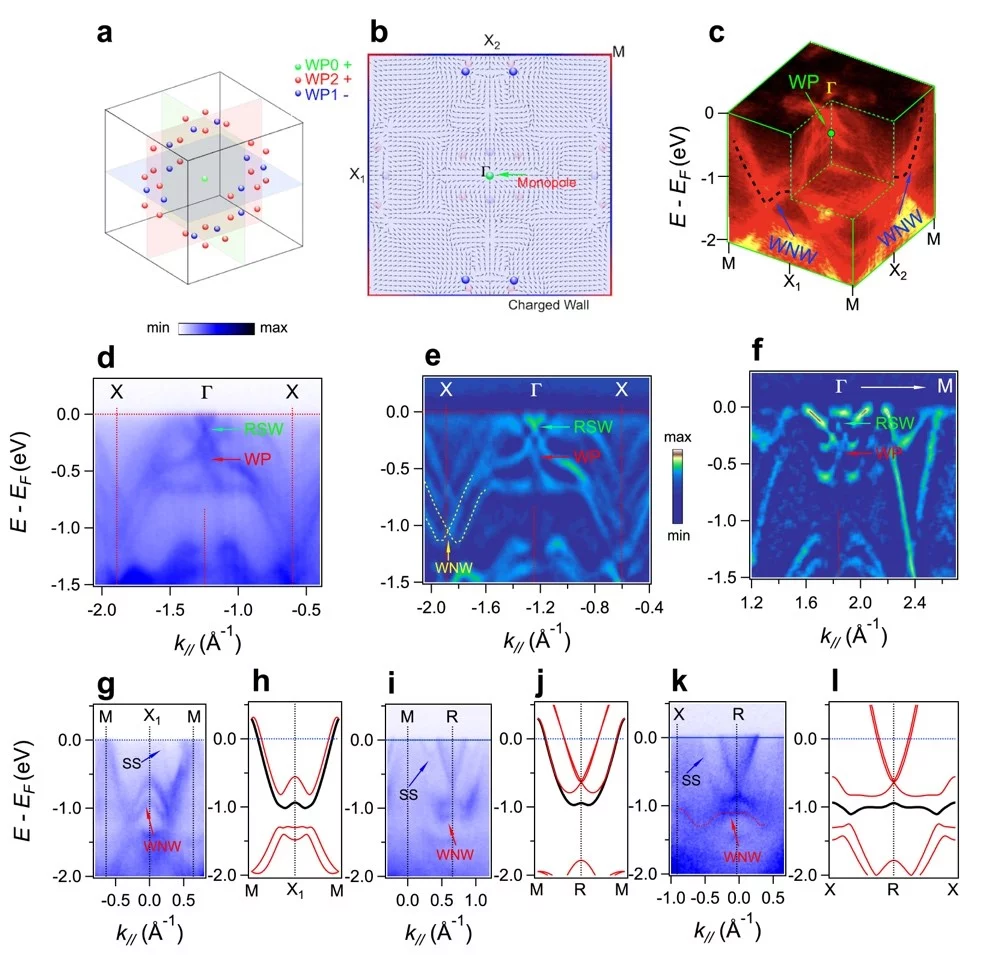
It is widely believed that the appearance of Weyl fermions in solids is restricted by the well-known Nielsen-Ninomiya no-go theorem proposed during the 1980s, which states that zero dimensional (0D) Weyl nodes in topological semimetals should always appear in pairs with opposite chiral charges in 3D momentum space. As a consequence, the projections of the Weyl nodes on the surface Brillouin zone are always connected by Fermi arcs. Considerable theoretical efforts have been dedicated to search for unpaired Weyl fermions beyond this no-go theorem, as such a discovery would carry major fundamental implications. One recent investigation suggests a path toward realizing these novel Weyl fermions by introducing a single Weyl point surrounded by symmetry-protected nodal walls on the Brillouin zone (BZ) boundary. The original no-go theorem is circumvented in this case as the Chern number in the 2D slices (which is a topological invariant that determines the appearance of a surface Fermi arc) of the 3D BZ is ill-defined. As a result, the Weyl points do not have to appear in pairs, and a surface Fermi arc connecting to the projection of the Weyl point is no longer necessary. Realizing such Weyl semimetal in solid materials, however, is considered a great challenge.

Combining angle-resolved photoemission spectroscopy (ARPES) with density functional theory calculations, a research team at PSI has revealed for the first time that unpaired Weyl points beyond the original no-go theorem can emerge in various compounds. In the promising candidate material PtGa, they observed that there is one unpaired Weyl point protected by time reversal symmetry at the BZ centre, and there are 36 unpaired accidental Weyl points at generic k points. These Weyl points are surrounded by topologically charged nodal walls on the BZ boundary. No surface Fermi arcs connecting the projections of the Weyl points have been observed. These observations demonstrate that, as a topological chiral charge, an unpaired magnetic monopole can be realized in the momentum space, which make the new class of topological semimetals distinct from all previously identified Weyl semimetals that all contain paired Weyl points.

Since the no-go theorem was derived in 1980s, this theorem doesn’t give any precise description and derivation for its application on the nodal surfaces which was only recently proposed. However, if one generalizes the no-go theorem to include different-dimensional topological objects, the extended no-go theorem is applicable for special cases of the concomitant coexistence of singular Weyl nodes and separated nodal lines or nodal walls. Thus, the unpaired Weyl points can be viewed as counterparts of the topologically charged Weyl nodal wall.

The discovery opens a new direction of research into topological materials in which nontrivial band crossings of 0D and 2D Weyl nodes emerge concomitantly and their coexistence ensures the net topological charge to be zero. The observation also extends the applicable range of the original Nielsen-Ninomiya no-go theorem, which was derived for only zero-dimensional paired Weyl Points with opposite chirality.