Exact solution of the classical and quantum Heisenberg mean field spin glasses

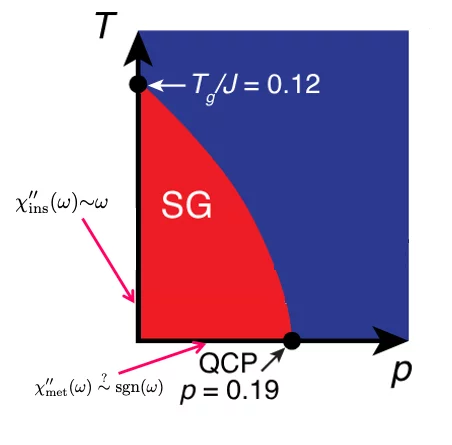
We present the numerically exact mean field solution of the quantum and classical problem in the limit of large connectivity, both for an undoped insulating glass (half-filled Mott insulator), and for a doped, metallic spin glass. The short time quantum dynamics of the insulating glass (SG) tend to the superuniversal form found so far in all insulating mean field glasses, with a spectral function $\chi’’(\omega)\sim \omega)$ at asymptotically low temperatures. The metallic  glass (doping fraction $p$) has yet more weight at low frequencies, its collective modes being random spin waves overdamped by the metallic fermions. Here the dynamics of the glass reflect the proximity to the melting quantum critical point (QCP) and its associated Planckian dynamics, with spectral features very similar to the marginal Fermi liquid behavior of the spin liquid regime of the Sachdev-Ye-Kitaev (SYK) model, $\chi’’(\omega)\sim {\rm sgn}(\omega)$. The latter was originally introduced as a large SU(M)  version of the insulating Heisenberg problem in its paramagnetic regime. Our exact $SU(M\to 2)$ solution now shows that SYK physics is hardly relevant in the insulating paramagnet, while, interestingly, the metallic glass exhibits very similar features as the SYK spin liquid, though for physically different reasons.