The Mu-MASS (MUoniuM lASer Spectroscopy) Experiment

Muonium is an exotic atom consisting of a positive anti-muon and an electron. Like hydrogen, this is a simple two-body system highly amenable to theoretical study. Therefore, studies of Muonium can be used to precisely determine muon properties, e.g., its mass and magnetic moment. In contrast to hydrogen and its proton constituent, muons and electrons, as part of the lepton family, have no internal structure. This makes Muonium free of finite size and nuclear effects. Without the theoretical complications introduced by these effects, Muonium is an exceptional testing ground for bound-state QED [1], as well as a strong candidate for hints of new physics that would have otherwise been masked by these effects.

Mu-MASS Logo

The Mu-MASS experiment [2] is pushing the forefront of Muonium laser spectroscopy and aims to measure the 1S-2S transition frequency of Muonium to an unprecedented precision of 10 kHz (4 ppt level), a 1000-fold improvement over previous measurements [3]! This will give the best determination of the muon mass at 1 ppb, critical for the g-2 experiment in which comparison with theoretical models is limited by our knowledge of this value [4,5,6]. Combining the Mu-MASS results with ongoing hyperfine measurements of Muonium (MUSEUM) at J-PARC [7] will provide one of the most sensitive tests of bound-state QED with a relative precision of 1x10-9 [8]. As well,the Rydberg constant will be determined independently of nuclear and finite-size effects at a level of 10-12 by combining the results of the MUSEUM and Mu-MASS experiments—an important result on its own that could also help to shed some light on the proton charge radius puzzle [9]. In regards to new physics, Mu-MASS will testcharge equality between the first two generations of charged leptons with a sensitivity of 1 ppt (3 orders of magnitude better than compared to the current limit [3]) that has recently been challenged by B-meson decays [10], and also serves as an exciting probe for the effect of gravity on anti-matter [11] as well as dark forces between electrons and muons [12].

Mu-Mass Laser

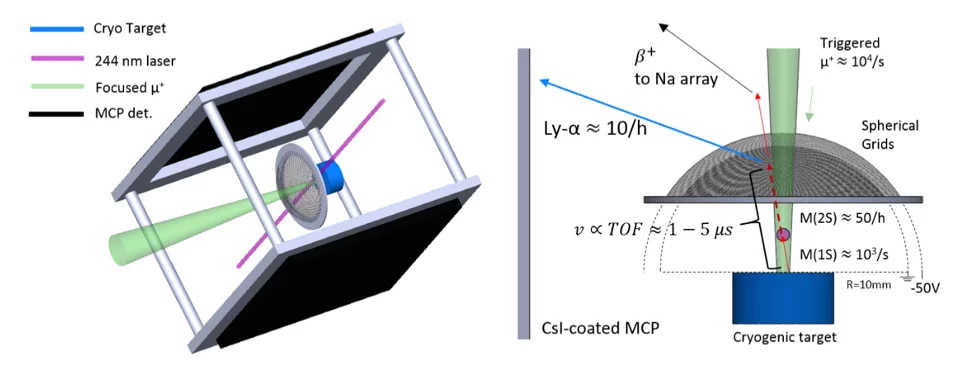
The Mu-MASS experiment will be built upon recent advances in cold Muonium (M) sources and UV laser technology. Novel cryogenic Mconvertersdemonstrated with the LEM beamline at PSI [13,14] are able to emit sizeable fractions of 100 K M into vacuum [15]. Meanwhile, tremendous advances in laser technology for the generation of UV laser light at the required frequency have been achieved [16,17], making orders of magnitude more CW light available for such an experiment. These two advances combined allows for the possibility of performing for the first time continuous wave (CW) laser spectroscopy of this transition, which was the main limitation of previous measurements [3]. Additionally, a successful 1S-2S measurement relies on the detection of the excited fraction M(2S) as a function of the absolute frequency of a strong VUV excitation laser. The current intended detection scheme for M(2S) draws upon demonstrated techniques utilized in hydrogen spectroscopy, namely quenching of M(2S) directly in a static electric field and efficiently detecting the emitted Lyman-Alpha (Ly-A) photons using MCP detectors.

Currently, these 3 ingredients for successful Muonium spectroscopy 1) Cold M Source, 2) High power CW UV laser at 244 nm 3) Efficient Lyman-Alpha detection have all been demonstrated by the Mu-MASS team. The goal of the next beamtime is to combine the laser and detection scheme with the cold M source at LEM and detect for the first time CW-laser excited Muonium atoms. 

Mu-Mass setup
  1. S. G. Karshenboim, Phys. Rep. 422, 1 (2005).
  2. P. Crivelli, Hyperfine Interact 239, 49, (2018).
  3. V. Meyer et al., Phys Rev. Lett. 84, 1136 (2000).
  4. T. Blum el al., arXiv:1311.2198 [hep-ph].
  5. W. Gohn, FERMILAB-CONF-17-602-PPD, arXiv:1801.00084 [hep-ex].
  6. M. Otani et al., JPS Conf. Proc. 8 025008 (2015).
  7. P. Strasser et al., Hyperfine Interact. 237, 124 (2016).
  8. A. Czarnecki, S. I. Eidelman, and S. G. Karshenboim Phys. Rev. D 65, 053004 (2002); S. Karshenboim et al., Nuclear Physics B (Proc. Suppl.) 162 260 (2006); M. I. Eides and V. A. Shelyuto, Phys. Rev. D 92 013010 (2015)
  9. R. Pohl et al., Nature 466, 213 (2010); A. Antognini et al., Science 339, 417 (2013).
  10. G. Ciezarek, M. Franco Sevilla, B. Hamilton, R. Kowalewski, T. Kuhr, V. Lu ̈th and Y. Sato, Nature 546, 227 (2017).
  11. S. Karshenboim, Astronomy Letters 35, 663 (2009).
  12. C. Frugiuele, J. Pérez-Ríos, C. Peset, Physical Review D, 100(1), 015010 (2019)
  13.  T. Prokscha, E. Morenzoni, K. Deiters, F. Foroughi, D. George, R. Kobler, A. Suter, and V. Vrankovic, Nucl. Instrum. Methods Phys. Res., Sect. A 595, 317 (2008).
  14. T. Prokscha et al., Physica B: Condensed Matter 404, 1007 (2009).
  15. A. Antognini, P. Crivelli, T. Prokscha, K. S. Khaw, B. Barbiellini, L. Liszkay, K. Kirch, K. Kwuida, E. Morenzoni, F. M. Piegsa, Z. Salman, A. Suter, Phys. Rev. Lett. 108, 143401 (2012).
  16. S. F. Cooper, Z. Burley, A. D. Brandt, C. Rasor and D. C. Yost, Optic Letters 43, 1375 (2018).
  17. Z. Burkley, A. D. Brandt, C. Rasor, S. F. Cooper, and D. C. Yost, Appl. Opt. 58, 1657-1661 (2019)
ERC logo