Mechanical response of stainless steel subjected to biaxial load path changes: cruciform experiments and multi-scale modeling

We propose a multi-scale modeling approach that can simulate the microstructural and mechanical behavior of metal or alloy parts with complex geometries subjected to multi-axial load path changes. The model is used to understand the biaxial load path change behavior of 316L stainless steel cruciform samples. At the macroscale, a finite element (FE) approach is used to simulate the cruciform geometry and numerically predict the gauge stresses. In fact, a uniaxial tension along one of the cruciform arms results in a biaxial stress state in the gauge region with tensile and compressive components along the loading direction and the second in-plane direction, respectively. Furthermore, both these stresses evolve non-linearly with respect to each other and the applied load, and cannot be computed analytically.

At each material point in the finite element mesh, the anisotropic viscoplastic self-consistent (VPSC) model is used to simulate the role of texture evolution on the mechanical response. At the single crystal level, a dislocation density based hardening law that appropriately captures the role of multi-axial load path changes on slip activity is used. The combined approach is experimentally validated using cruciform samples subjected to uniaxial load and unload followed by different biaxial reloads in the angular range [27°,90°]. Polycrystalline yield surfaces (PCYS) before and after load path changes are generated at different strain values using the full-field elasto-viscoplastic fast Fourier transform (EVP-FFT) model. These are useful to study the influence of the deformation history and reloading direction on the mechanical response, including the Bauschinger effect, of these cruciform samples.

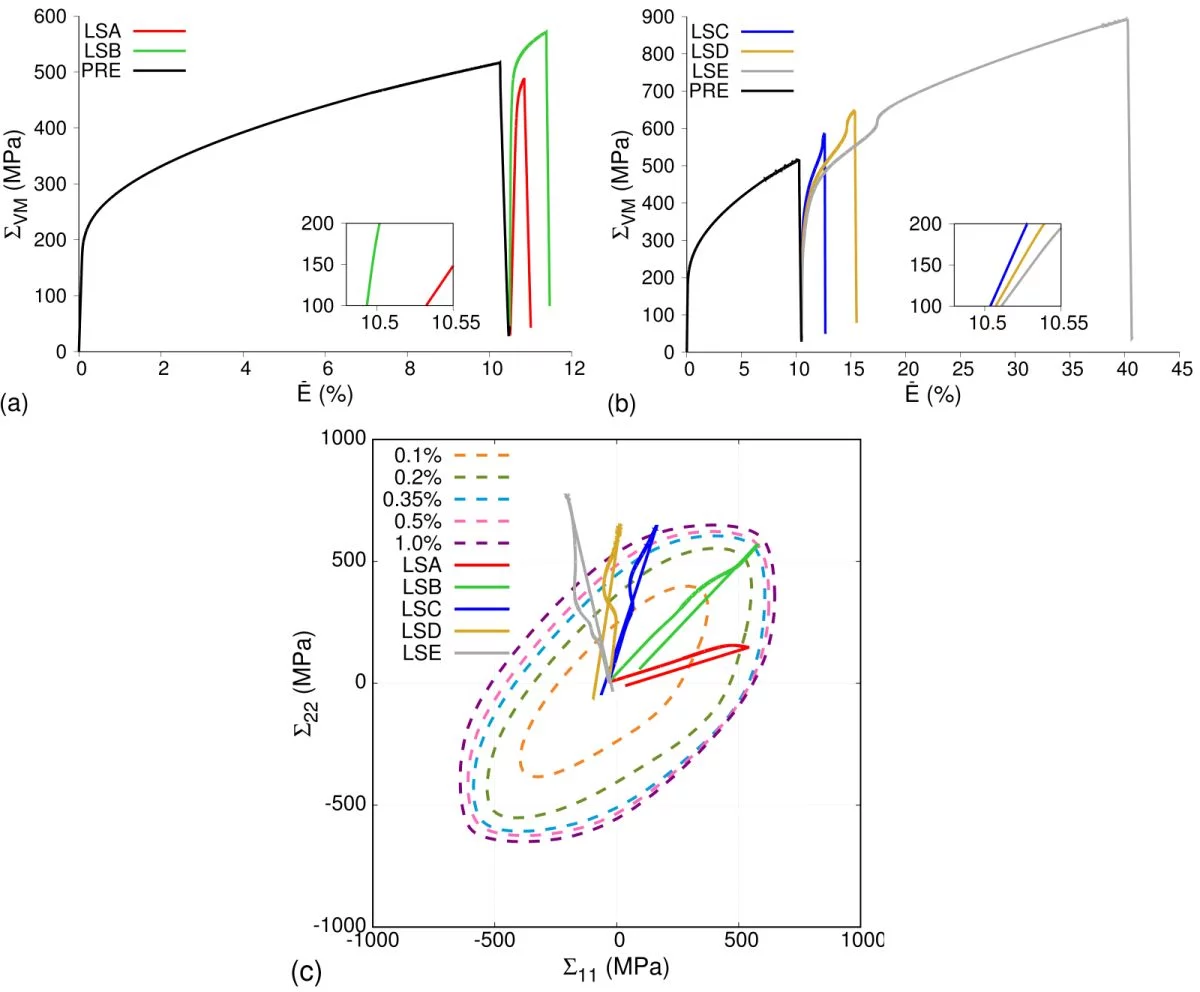
In figure 1a and b, we have plotted the von Mises stress v/s accumulated total von Mises strain for the 5 different biaxial load path changes after a horizontal uniaxial tensile load and unload viz. LSA (reload at 27°), LSB (45°), LSC (63°), LSD (71°) and LSE (90°). It can be seen that the equibiaxial load path change (LSB) has the elastically stiffest and plastically hardest response in the initial stages of reload. This can be explained with the help of PCYS after the uniaxial load and unload shown in figure 1c. These are also superimposed with the gauge stress evolution following a load path changes for different biaxial load path changes. Figure 1c shows that the PCYS has bulged along the direction of the uniaxial load as well as the equibiaxial tension. This explains why the equibiaxial reload has the stiffest and hardest response.

Interestingly, the bulge in PCYS rapidly vanishes with increasing deformation indicating that the Bauschinger effect is strongly dependent on the first loading direction and strain, intergranular and macroscopic residual stresses after first load, and the reloading angle, but not on the dislocation structure evolution after a load path change. The microstructural origins of the mechanical response, particularly the dislocation density evolution, are studied. Further details can be found in the publication indicated below.