Was der Satz vom Igel über Flussschläuche in Supraleitern sagt

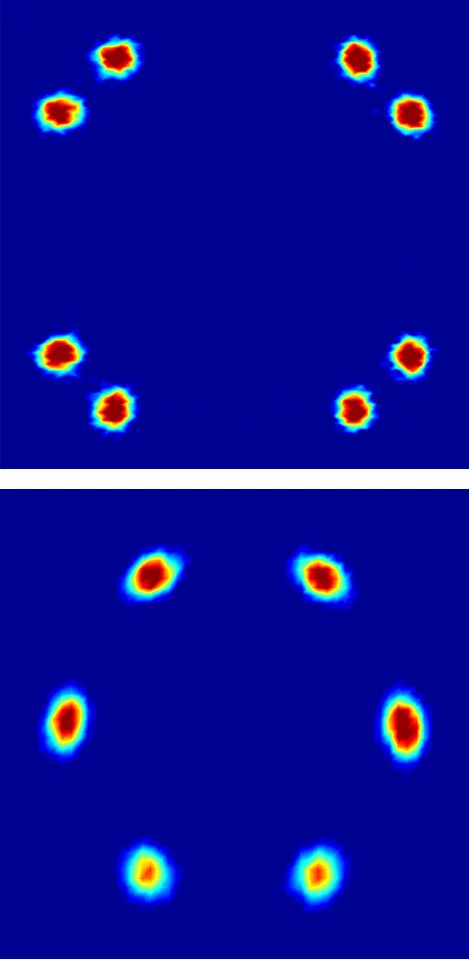
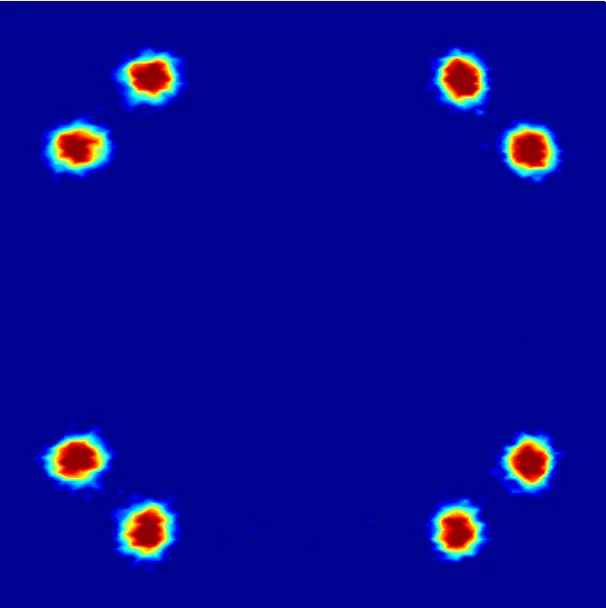
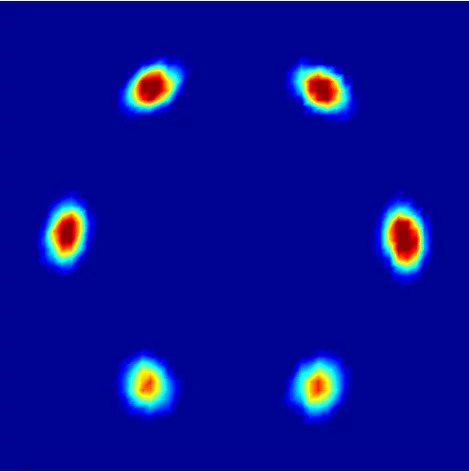
Supraleiter sind vor allem dafür bekannt, dass sie elektrischen Strom ohne Widerstand leiten. Eine andere wichtige Eigenschaft dieser Materialien ist, dass sie kein Magnetfeld in ihrem Inneren vertragen – bringt man sie in ein äusseres Magnetfeld, so leiten sie es aussen herum und halten ihr Inneres feldfrei. Die Supraleiter vom Typ II – die so genannten Hochtemperatursupraleiter – haben noch eine weitere Möglichkeit, sich vor Magnetfeldern zu schützen. Sie können so genannte Flussschläuche bilden, in denen das Magnetfeld durch das Innere des Supraleiters geleitet wird. In den Kernen der Schläuche ist dann das Material nicht mehr supraleitend, aber überall ausserhalb – das Material gibt gewissermassen die Supraleitung für einen Teil seines Inneren ab, um sie für den Rest zu retten. Macht man das äussere Magnetfeld stärker, entstehen mehr Flussschläuche – bei sehr starkem Magnetfeld bricht die Supraleitung ganz zusammen. Die Flussschläuche sind parallel zum äusseren Magnetfeld und ordnen sich meist in regelmässigen Mustern. Die Anordnung der Flussschläuche lässt sich mit Neutronenexperimenten bestimmen, wie sie an der Neutronenquelle SINQ des Paul Scherrer Instituts durchgeführt werden.

Verschiedene Muster für verschiedene Richtungen

Schon vor rund 30 Jahren hatten Forscher in den USA beobachtet, dass sich die Anordnung der Flussschläuche in dem supraleitenden Schwermetall Niob ändert, wenn man es im Magnetfeld dreht. Deren Anordnung hängt also davon ab, in welche Richtung das Magnetfeld durch den Supraleiter dringt. Diese Untersuchungen wurden in den vergangenen Jahren von verschiedenen Gruppen vor allem mit Untersuchungen an Niob wieder aufgenommen und es bestätigte sich: drehte man einen Niob-Kristall im Magnetfeld, so änderte sich plötzlich das Muster der Flussschläuche oder das Muster ging gar ganz verloren, so dass die Flussschläuche unregelmässig verteilt waren. Dass das nicht eine Besonderheit von Niob ist, sondern wegen einer fundamentalen mathematischen Gesetzmässigkeit – dem Satz vom Igel – so sein muss, haben nun die beiden Forscher Mark Laver vom Paul Scherrer Institut und Edward. M. Forgan von der Universität Birmingham gezeigt.

Der Satz vom Igel

Jeder stetig gekämmte Igel hat mindestens einen Glatzpunkt. ist die populäre Formulierung des mathematischen Satzes vom Igel – der offenbar von Mathematikern so benannt wurde, die mit Igeln wenig vertraut waren und nicht erkannten, dass man die Stacheln eines Igels nicht kämmen kann. Da beschreibt der englische Name Hairy ball theorem den Sachverhalt treffender. Der besagt in etwa, dass wenn man eine behaarte Kugel kämmt, es immer mindestens einen Punkt geben wird, der nicht von Haaren bedeckt ist. Wobei die Haare kurz sein müssen und die Frisur stetig – die Haare an nahegelegenen Punkten sollen in ähnliche Richtungen zeigen. Eine zerraufte Kugel würde das Problem also nicht lösen. Dieser Satz hat in vielen Gebieten weitreichende Folgen – zum Beispiel folgt daraus, dass es auf der Erde stets mindestens einen Punkt geben muss, an dem kein Wind weht, wobei hier die Windrichtungen an den verschiedenen Punkten den Haaren der Kugel entsprechen.

Die Überlegung

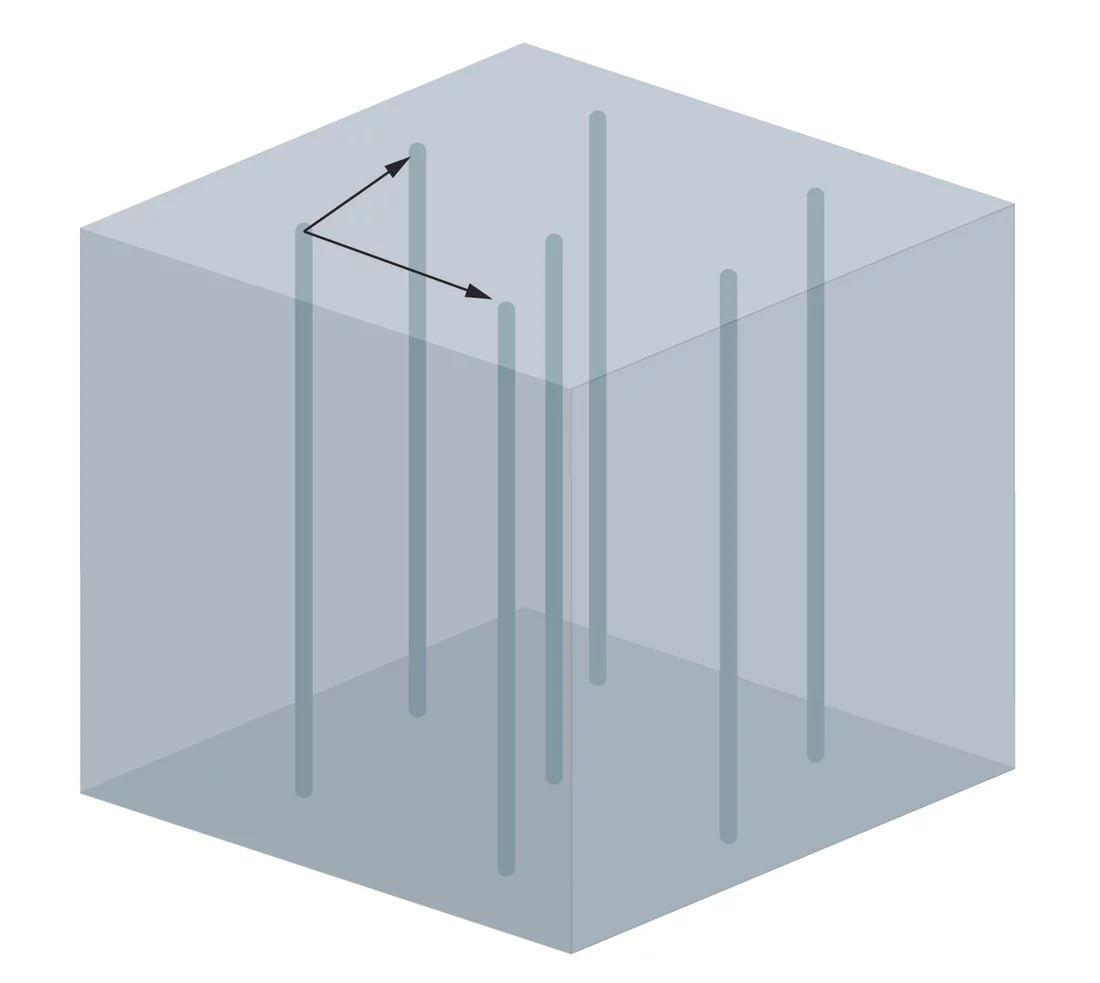
Hinter dem Zusammenhang zwischen dem Satz und den Flussschläuchen steckt folgende mathematische Überlegung: Man kann das äussere Magnetfeld, das an den Supraleiter angelegt wird, als einen Pfeil (Vektor) darstellen, dessen Richtung der Richtung des Magnetfelds entspricht und dessen Länge die Stärke des Magnetfelds repräsentiert. In dem Experiment wird die Richtung des Magnetfelds variiert, dessen Stärke bleibt gleich – das heisst, die Vektoren sind immer gleich lang. Stellt man sich vor, dass die Vektoren für alle Richtungen am gleichen Punkt im Raum beginnen, so liegen die Enden der Vektoren alle auf einer Kugeloberfläche. Das ist die Kugeloberfläche, die man für den Satz vom Igel braucht.

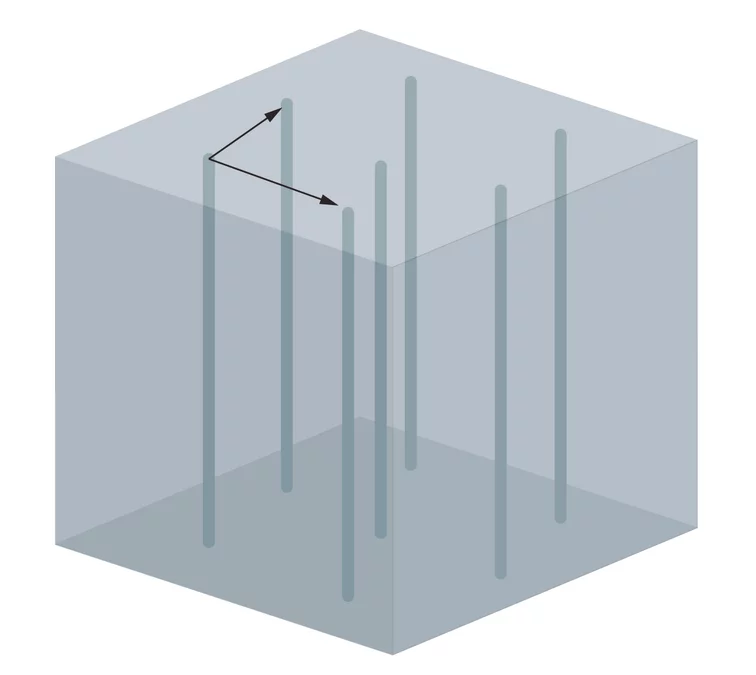
Die Flussschläuche im Supraleiter sind immer parallel zum äusseren Magnetfeld. Sind sie in einem typischen regelmässigen Muster angeordnet, kann man dieses Muster durch zwei Pfeile oder Vektoren beschreiben. Dazu wählt man einen beliebigen Flussschlauch aus und betrachtet einen Vektor, der zu diesem Schlauch senkrecht ist und bis zu einem der nächstgelegen Flussschläuche zeigt. Insgesamt gibt es mehrere solche Vektoren, aber es reichen zwei aus, die nicht zueinander parallel sind, um die gesamte Anordnung der Flussschläuche zu bestimmen. Man muss einfach an einem Flussschlauch anfangen, da einen solchen Vektor anlegen und am Ende des Vektors ist dann wieder ein Flussschlauch, an den man wieder einen Pfeil anlegen kann und so weiter. Diese Vektoren sind jetzt die Haare der haarigen Kugel – je zwei an jedem Punkt.

Nimmt man jetzt an, dass das Muster der Flussschläuche für alle Magnetfeldrichtungen gleich bleibt, stösst man auf einen Widerspruch. Denn das würde bedeuten, dass die Vektoren, die benachbarte Flussschläuche verbinden, sich für nahe gelegene Punkte nur wenig unterscheiden. Und das ist nach dem Satz vom Igel nicht möglich.

Physikalisch gesehen ist auch klar, dass die Muster nicht gleich sein müssen, da nicht alle Richtungen gleichberechtigt sind – schliesslich hat der Supraleiter ein Kristallgitter, das bestimmte Richtungen auszeichnet.

Verschiedene Lösungen

Die Natur löst das Problem auf verschiedene Weise. Die eine Möglichkeit ist, dass sich das Muster sprunghaft ändert, wenn man die Richtung des Magnetfelds ändert. Eine andere Möglichkeit ist, dass die Flussschläuche unregelmässig angeordnet sind – also kein regelmässiges Muster bilden und damit auch keine Vektoren an der Kugeloberfläche festlegen. Bisweilen gibt es auch zwei Muster, die einander durchdringen.

Schub ähnlich wie die Einführung der Computertomografie

Der Satz vom Igel macht deutlich, wie wichtig die Untersuchung der winkelabhängigen Eigenschaften von Flussschläuchen in Supraleitern ist. Für das Verständnis der Supraleitung könnte das einen ähnlichen Schub bedeuten wie die Einführung der Computertomografie in der Medizin schätzt Mark Laver die Bedeutung seiner Arbeit ein.

Text: Paul Piwnicki

Über das PSI

Das Paul Scherrer Institut entwickelt, baut und betreibt grosse und komplexe Forschungsanlagen und stellt sie der nationalen und internationalen Forschungsgemeinde zur Verfügung. Eigene Forschungsschwerpunkte sind Festkörperforschung und Materialwissenschaften, Elementarteilchenphysik, Biologie und Medizin, Energie- und Umweltforschung. Mit 1400 Mitarbeitenden und einem Jahresbudget von rund 300 Mio. CHF ist es das grösste Forschungsinstitut der Schweiz.