La physique sur réseau : mieux comprendre les gaz confinés

Cela fait des lustres que les physiciens utilisent l’équation de Boltzmann pour décrire le comportement des gaz. Toutefois, à ce jour, on n’a toujours pas réussi à trouver à cette même équation une solution mathématique exacte, universellement valable. A défaut de solution, que l’on pourrait noter au crayon sur du papier, les scientifiques ont opté pour la voie qui leur restait : celle des calculs informatiques. C’est de cette nécessité qu’est née la méthode de Boltzmann sur réseau (appelée aussi Lattice Boltzmann Method).

Diviser pour régner

L’équation de Boltzmann est une tentative réussie de saisir à l’aide de statistiques la « vie intérieure » particulièrement complexe d’un gaz. Cela signifie qu’au lieu de suivre chaque molécule dans son mouvement chaotique, on calcule la probabilité qu’un certain nombre de molécules se trouve dans une location donnée d’espace et de vitesse.

La méthode de Boltzmann sur réseau simplifie également le problème grâce à l’artifice de la discrétisation : au lieu de suivre le mouvement de la molécule de gaz dans l’ensemble du continuum spatial, on se contente de connaître le comportement des molécules en certains points. Le continuum spatial est donc remplacé par une grille (réseau) constituée de ces mêmes points, ce qui réduit la quantité des calculs nécessaires.

Il suffit en effet de savoir, à chaque moment, si une molécule se trouve en un certain point du réseau et, le cas échéant, à quelle vitesse et dans quelle direction cette même molécule se déplace. L’évolution temporelle de l’état du gaz est ensuite exécutée chaque fois en deux étapes. D’abord, toutes les molécules sont déplacées au point suivant du réseau, en fonction de la direction de leur mouvement. Deuxièmement, là où des molécules se heurtent, leur collision est réalisée, ensuite de quoi ces molécules adoptent de nouvelles directions et de nouvelles vitesses.

Par ailleurs, les changements qui surviennent en un point du réseau ne peuvent se produire qu’au travers de l’influence des points du réseau qui se trouvent dans son voisinage immédiats : ce fait réduit encore la quantité de calculs nécessaires. On constitue donc au sein du réseau des cellules, isolées du reste de l’espace de réseau. Et c’est précisément là que réside un avantage important de la méthode de Boltzmann sur réseau : les calculs pour la cellule seule peuvent s’effectuer indépendamment les uns des autres, et simultanément sur de nombreux processeurs. Cette division (parallélisation) réduit fortement l’investissement temps, en fonction du nombre de processeurs disponibles.

Déployer ses forces quand l’espace vient à manquer

Dans de nombreuses situations, la méthode de Boltzmann sur réseau offre une bonne alternative aux instruments établis de simulations de dynamique des fluides. Mais elle déploie tout particulièrement ses forces dans la description de ce que l’on appelle la microfluidique. La microfluidique intervient par exemple au sein de petits convertisseurs d’énergie, comme les piles à combustible pour appareils portables, et dans la plupart des catalyseurs techniques. Dans des systèmes de ce genre, les gaz ou les liquides doivent se déplacer dans un espace très restreint, ou franchir des pores microscopiques. Les processus de dynamique des fluides doivent être ensuite décrits au niveau de chaque particule. Or, comme la méthode de Boltzmann sur réseau est précisément basée sur une théorie microscopique des processus de dynamique des fluides, elle est comme prédestinée à trouver une application dans ce genre de questionnements.

Mais pour aboutir à sa maturité actuelle, cette méthode de simulation a dû parcourir un long chemin. « Il y a 20 ans, les possibilités qu’elle offrait étaient vraiment limitées », explique Ioannis Mantzaras, chef du groupe Fondements de la combustion au PSI. A elle seule, sans l’aide d’autres instruments, la méthode de Boltzmann sur réseau, ne permettait pratiquement que de décrire des substances pures à température constante. Or ce cas de figure est bien entendu souvent très éloigné de la réalité.

Des simulations toujours plus réalistes

Toutefois, au cours des dernières années, grâce à l’accélération du développement de la performance de calcul et de la capacité de stockage des ordinateurs, mais aussi grâce au raffinement des processus de calcul (algorithmes) et des modèles physiques, des possibilités sont apparues, qui étaient inconcevables auparavant. En appliquant la méthode de Boltzmann sur réseau, les scientifiques sont aujourd’hui en mesure d’étudier sur ordinateur, de manière réaliste, des systèmes très complexes, moyennant un effort raisonnable.

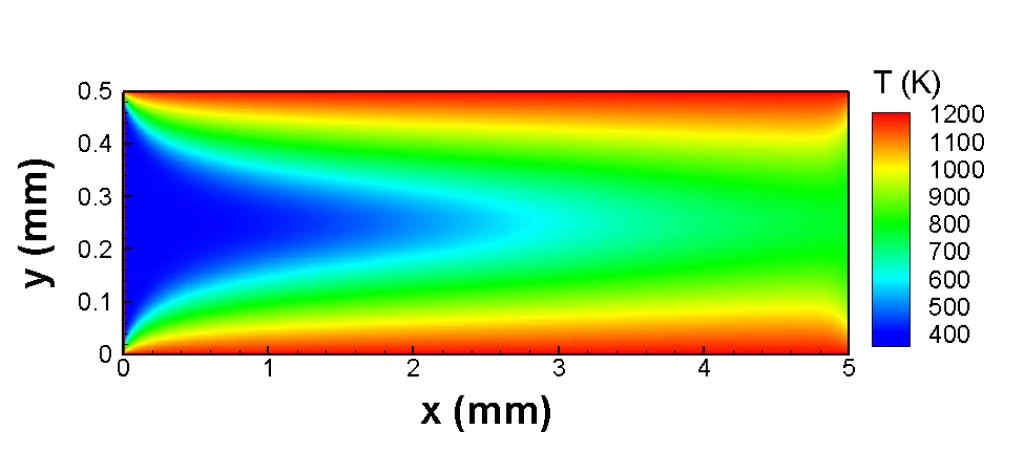
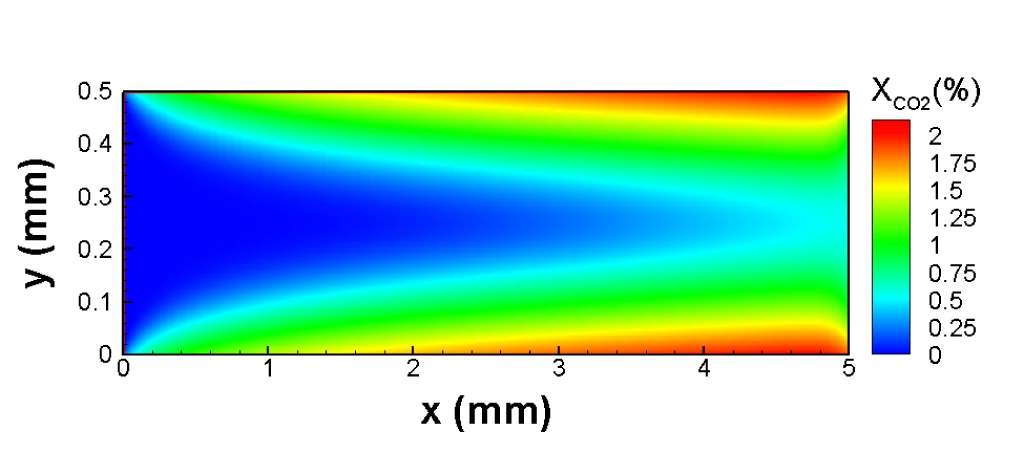
Une évolution dont profitent aussi les chercheurs du PSI. Ils ont à présent développé pour la première fois un modèle, qui permet de simuler l’écoulement de mixtures gazeux ou liquides à des températures variées, au moyen de la méthode de Boltzmann sur réseau. Pour ce faire, ils ont dû remédier à un sérieux défaut du modèle de réseau utilisé jusque là pour les mixtures, à savoir son incapacité à décrire simplement une loi de la nature aussi importante que la conservation de l’énergie. Les chercheurs y sont parvenus, en modélisant adroitement les collisions entre les molécules de gaz.

Améliorer les simulations, diminuer les coûts de développement

Avec leur travail, les scientifiques du PSI ouvrent la voie à des simulations informatiques plus réalistes de nombreux processus techniques complexes. « Les mixtures gazeux présentant des différences de température interviennent dans de nombreux systèmes techniques, par exemple dans les structures microporeuses de catalyseurs techniques, dans les filtres à particules diesel, les microréacteurs à combustion, ou encore dans les piles à combustible, explique Nikolaos Prasianakis, qui a contribué au développement du modèle. Comme il est maintenant possible de simuler ces systèmes sur ordinateur, nous contribuons à ce qu’à l’avenir les coûts de développement diminuent. On peut en effet jouer davantage de scénarios sur ordinateur que dans le cadre de vrais tests, lors desquels des prototypes coûteux sont détruits ou endommagés. Aujourd’hui, par exemple, plus aucune voiture n’est testée en tunnel aérodynamique, avant que son comportement aérodynamique n’ait été simulé sur ordinateur de manière approfondie. » Les expériences restent indispensables, mais grâce aux simulations, elles peuvent être planifiées et conduites de manière plus efficace.

Validation détaillée

Les tests de validation d’un modèle de simulation, aussi exact soit-il d’un point de vue mathématique, sont indispensables eux aussi. Raison pour laquelle les chercheurs du PSI ont testé en détail si leur modèle restituait correctement le comportement des écoulements simulés. Ils ont ainsi pu démontrer, par exemple, que leur méthode décrivait correctement les modifications de la vitesse de propagation du son dans un gaz en fonction de la température. Dans d’autres tests, ils ont montré que leur modèle fournissait des résultats, qui coïncidaient avec ceux d’autres méthodes de simulation établies. Le modèle a également tenu la comparaison dans les cas où une solution mathématique exacte était déjà connue. Sous sa forme publiée, leur modèle ne vaut, à présent, que pour des courants en deux dimensions d’un mixture de gaz composé de deux substances chimiques. Mais les chercheurs ont montré que leur modèle pouvait être élargi à trois dimensions, et à des mélanges constitué d’un nombre illimité de composants.

Texte : Leonid Leiva